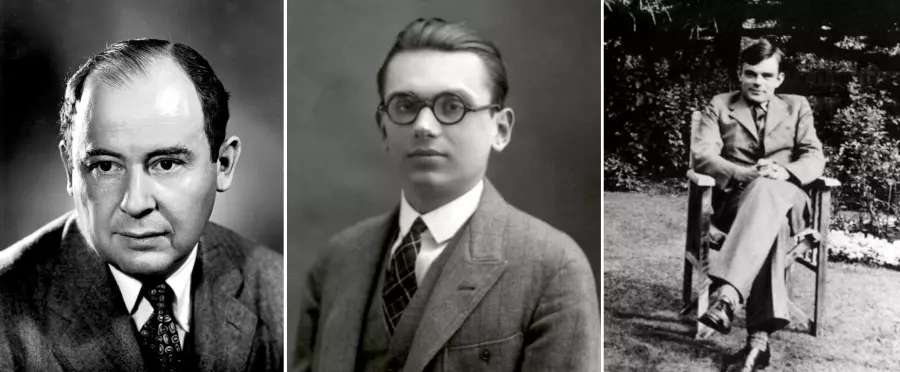
Byli Kurt Gödel a Alan Turing ideoví oponenti? Zapojíme-li do filosofických úvah ještě třetího aktéra Johna von Neumanna, jehož umístíme na první místo, zjistíme, že se některé úvahy u všech tří zmíněných filosofů shodují. Přečtěte si další příspěvek, který vznikl v rámci spolupráce portálu Vědavýzkum.cz a časopisu Teorie vědy, jehož autory jsou Barbora Jurková a Lukáš H. Zámečník z Filozofické fakulty Univerzity Palackého.
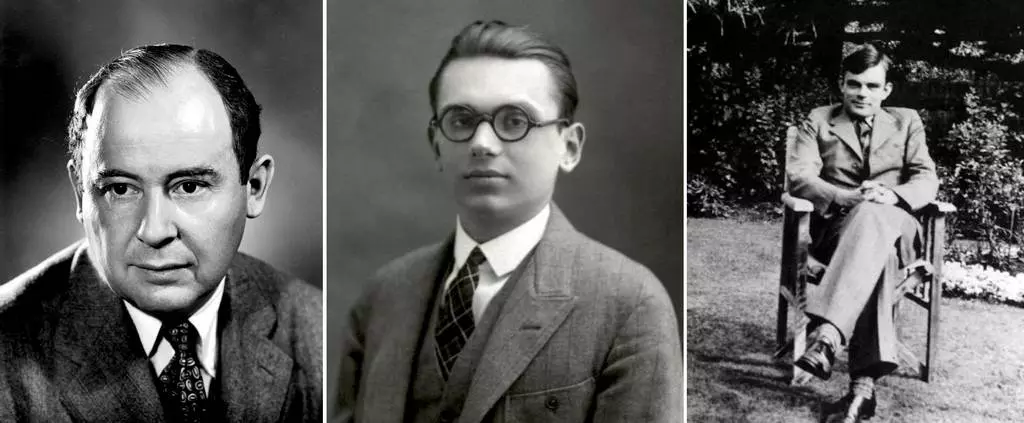
Foto: Zleva John von Neumann, Kurt Gödel a Alan Turing. Foto: Wikipedia
V debatách a textech filosofů často vystupují Kurt Gödel a Alan Turing jako ideoví oponenti. Na mysli vytane přelomová představa „myšlení jako výpočtu“, filosoficky rozvinutá v koncepci Turingova testu, oproti Gödelovu opět přelomovému zjištění o „neúplnosti matematiky“, často využívanému k dovozování, že mysl je něco víc než jen výsledek činnosti stroje (J. R. Lucas, R. Penrose). John von Neumann se naopak v úvahách filosofů nevyskytuje příliš často, navzdory tomu, že jeho jméno nalezneme pod nepřeberným množstvím vědeckých zjištění napříč vědními disciplínami, matematiku a umělou inteligenci nevyjímaje. Mezi nejznámější patří jeho práce týkající se prototypu EDVAC, účast v projektu Manhattan, či teorie her v ekonomii (ale zásadně přispěl také v kvantové fyzice, teorii množin ad.).
Cílem našeho článku je ukázat, že uváděná opozice neplatí, a že zapojíme-li do filosofických úvah i třetího aktéra a umístíme-li jej na první místo trojice uvedené v názvu, pak:
- porozumíme tomu, jakou úlohu sehrála logika a matematika pro porozumění kódu (nejen ve výpočetní vědě, ale například i v biologii);
- zjistíme, že úvahy o mysli ve vztahu k výpočetnímu stroji se objevují u všech tří myslitelů v překvapivé shodě.
Na první pohled nesourodé věci, jako je Gödelova neúplnost systému, Turingovo hledání univerzálního algoritmu a von Neumannova snaha o konstrukci sebe-replikačního stroje se v našem článku propojují do uceleného obrazu konstrukce kódu, který vyžaduje odlišování syntaxe a sémantiky formálního systému. A toto odlišení je klíčové i pro druhou rovinu našeho zkoumání, jehož jádro vystihuje Gödelovo překvapivé prohlášení, že: „Mysl je stroj, který pozná, že má pravdu.“ (Wang, Logical Journey, 189) Nejenom Turing a von Neumann, ale i Gödel chápali koncept výpočetního stroje ve vztahu k porozumění mysli jako centrální.
Protože nevycházíme jen z akademických publikací zkoumaných autorů, ale i z dalších dokumentů, které přibližují jejich vědeckou činnost, objevujeme i dobovou podmíněnost jejich vzájemných vztahů. Čerpali jsme z vybrané osobní korespondence, záznamů jejich přednášek (archiv Goldstine) a rozhovorů (Kurt Gödel a Hao Wang, Turing v BBC), či biografií (Stephen Budiansky o Kurtu Gödelovi, Andrew Hodges o Alanu Turingovi, Norman Macrae o Johnu von Neumannovi). Že mají všichni tři hlavní aktéři mnohem více společného, než by se na první pohled zdálo, je dokládáno na některých nově zveřejněných materiálech z digitalizovaných archivů, vzájemné korespondence a poskytnutých rozhovorů třetím stranám. Vyvstává tak plastický obraz nejen intelektuální výměny mezi vědeckými génii, ale i historických a společenských souvislostí, do kterých byli naši hrdinové vpleteni.
Je potřeba odlišovat syntax a sémantiku
Hlavním cílem článku je poskytnout čtenáři ucelený pohled na vznik konceptu kódu, který vedl k objevení rozdílných výpočetních strojů a dal vzniknout některým palčivým otázkám ve filozofii mysli, které (nejen) odbornou veřejností rezonují dodnes. Pro všechny tři autory je základem zjištění, že je třeba ve formálním systému odlišovat syntax a sémantiku. Nejde nám o to rekapitulovat celé důkazy a objevy, ale především poukázat na některé detaily, které je propojují.
Vše začíná u rakouského matematika Kurta Gödela a jeho příspěvku v Královci (1930), kterým odpovídá na Hilbertův program a dokazuje neúplnost formálního systému. Podstatnou součástí Gödelova důkazu je procedura (Gödelovo číslování), která umožňuje převést libovolné vyjádření v jazyce formálního systému na jedno – i když poněkud dlouhé – popisné číslo. Gödelovi se tak podařilo dokázat, že pravdivost (sémantická rovina) matematické věty nemusí implikovat existenci důkazu (syntaktická rovina) této věty a že tudíž formální systém je buď úplný, ale nekonzistentní, nebo zůstane konzistentním za cenu neúplnosti.
Britský matematik Alan Turing na Gödela a jeho systém číslování odkazuje hned na prvních stránkách svého článku (On Computable Numbers with an Application to the Entscheidungsproblem z roku 1937), jen celý postup „gödelizace“ přesouvá na úroveň hledání algoritmu, který by dokázal vyhodnotit, zda je daný komplexní formální systém rozhodnutelný a proceduru se mu daří vyjádřit skrze výpočetní postup abstraktního stroje. Turingovu univerzálnímu automatu je předložen ke zpracování seznam popisných čísel existujících automatů a čeká se, zda se stroj zastaví či zacyklí. Podstatné je to, že v rámci popisného čísla automatu se skrývají veškeré informace včetně toho, jak automat vyhodnotí problém, kterým se zabývá. V okamžiku, kdy univerzální automat dostává k vyhodnocení i vlastní zápis (ten musí v seznamu také existovat), jeho vyhodnocení vede k zacyklení stroje. Jde o to, že v rámci tohoto zápisu jsou obsaženy opět veškeré zápisy všech automatů, takže i přesto, že je dopředu rozhodnuto, že univerzální automat je necyklický, zacyklí se právě v tomto bodě, kdy pořád dokola bude vyhodnocovat seznam v rámci vlastního zápisu.
U Turinga se rozdíl mezi sémantikou a syntaxí pojí s odlišováním akceptovatelnosti a rozhodnutelnosti množiny řetězců (seznamů čísel). Pokud je řetězec rozhodnutelný, je automaticky i akceptovatelný, ale akceptovatelnost sama negarantuje ve všech případech rozhodnutelnost řetězce. Podstata obou důkazů spočívá v tom, že Gödel a Turing přišli s jedinečným způsobem, jak reprezentovat něco něčím jiným, v našem případě prvky formálního systému a jednotlivé automaty skrze sekvenci čísel. Objevili tedy kód. A díky tomu pravdivé a současně nedokazatelné věty, stejně jako univerzální automat, o kterém dopředu víme, že nemůže rozhodnout, přestávají působit dojmem paradoxu. Dvojí sada kódu – reprezentované a reprezentující – řeší problém bludného kruhu autoreference.
U maďarsko-amerického matematika Johna von Neumanna se odlišení sémantiky a syntaxe vyskytuje také. Jde o odlišení reprezentovatelnosti (sémantika) a konstruovatelnosti (syntax) sebereplikujícího se stroje. Von Neumann pokládá poměrně jednoduchou otázku: Je možné, aby stroj postavil svou kopii, má-li k tomu vše potřebné? Za vším potřebným se ovšem neskrývá jenom materiál, ale především kód. Proto, aby sebereplikace byla možná, je nutná existence kódu: musíme reprezentovat něco – v tomto případě části automatu, jejich propojení a funkce – něčím jiným – potřebujeme kód. U Turinga a Gödela je kód řešením problému autoreference, u von Neumanna je kód podmínkou sebereplikace systému (a zde pak začínají i implikace pro biologii).
S ohledem na pojetí mysli se naši tři protagonisté na první pohled výrazně liší. Gödel se opakovaně vyjadřoval proti (dnešními slovy) programu umělé inteligence. Je pro něj nepředstavitelné, že by stroj dokázal napodobit lidskou mysl. Turing chce naopak zbavit pojem mysli jeho bezprostřední vazby na lidské myšlení, konceptuální analýzou chce stanovit jeho strojově-vyjádřitelnou úroveň. Von Neumann jde ještě o kousek dál, je fascinován tím, jak funguje samotná nervová soustava a tvrdí, že matematika je jazyk mysli a že by to měla být právě matematika, která by nám měla pomoci při hlubším zkoumání nervové soustavy (Von Neumann, The Computer and the Brain).
Domníváme se, že většina tradičně uváděných radikálních odlišností mezi pojetím mysli u Gödela a Turinga ulpívala na nepochopení těchto jednoduchých rozdílů. Odhalení společné distinkce syntaxe a sémantiky vyjádřené v konceptu kódu nám přináší pochopení, že v jádru se zkoumaní autoři shodují – odlišují je pouze různé intuice o tom, co by měla být lidská mysl, respektive o tom, co si o mysli můžeme dovolit tvrdit.
Osudové momenty
Vědecká praxe se ovšem netýká jen velkých objevů, analýzy důkazů, vyvrácení mylných názorů, ale i osobních příběhů, životních událostí a osudových momentů. A právě ty posledně jmenované dodávají našemu článku určitý emocionální rozměr.
Královec a nepublikování von Neumannova důkazu
Náš příběh vlastně začíná v Královci, nějak až dojemně filosoficky čarovném městě. Vzpomeňme na jeho mosty, po kterých chodil Euler, po něm Kant a po něm i náš Kurt Gödel s Johnem von Neumannem. Setkávají se zde úplně poprvé v roce 1930, když von Neumann zavítá na Gödelovu přednášku „o neúplnosti matematiky“. Von Neumann je silně zaujat a to už i proto, že sám v dané době na podobném důkazu pracuje. Mezi oběma dojde k výměně několika dopisů, na jejímž konci von Neumann gentlemansky upouští od publikování své verze důkazu (my ji čtenáři v článku poskytujeme v Apendixu, pozn. autorů).
Protože víme, jaké to bylo v následujících dvou desetiletích s von Neumannem dále, je zmiňovaná epizoda podstatná. A proto také umisťujeme von Neumanna na první místo naší trojice géniů. Von Neumann přispěl tolika vhledy do natolik disparátních oblastí poznání, jež všechny přesáhl, že mu nečinilo obtíž v některých případech přenechat prvenství jiným. Von Neumann byl dost často k práci přizván či se sám nabídl jako konzultant, a díky svému intelektu byl schopen najít řešení či poskytnout pohled na danou problematiku. Asi nejznámější von Neumannův počin v oblasti tehdejších počítačů je jeho First Draft of a Report on the EDVAC, který společně s ním vypracoval Herman Goldstine. Byl to právě Herman Goldstine, kdo von Neumannovi řekl o probíhajícím projektu ENIAC a von Neumann se ze zvědavosti stal konzultantem (Goldstine, Herman H. The computer from Pascal to von Neumann). Tím nijak nesnižujeme význam ostatních členů vysněné trojice. Jen někteří z nich měli to štěstí, že nebyli v hledáčku úřadů, aby neprozradili utajované informace.
A tak musíme připustit, že génius sice může být sociálně konstruován, ale také může být stejně efektivně sociálně-politicky důkladně ukryt před zraky veřejnosti.
Von Neumann umírá a Gödel mu píše poslední dopis
Kontakt mezi Gödelem a von Neumannem neustal ve 30. letech. Už vzhledem k tomu, že von Neumann patřil mezi ty, kteří Gödelovi pomohli přesídlit po vypuknutí války do USA a uchytit se v akademickém prostředí na Princetonu. A tam se také z Gödela a von Neumanna stávají kolegové. Jistě, nové hollywoodské velkofilmy nám ochotně zopakují dojemný příběh procházek Gödela s Einsteinem, ale měli bychom si připomínat, že některé z nich zřejmě trávil Gödel i s géniem, který pomalu snoval představy o umělém životě a konstrukci sondy.
K poslednímu kontaktu mezi Gödelem a von Neumannem dochází v roce 1956, když už John von Neumann leží na smrtelné posteli v nemocnici (stále hlídán vládními úředníky díky svým vazbám na tehdejší vládu a některé významné instituce a jejich strachu, že by v blouznění mohl vyzradit utajované skutečnosti). Gödel na dopis, ve kterém naráží na palčivé problémy Turingova univerzálního stroje a ptá se von Neumanna na jeho názor (nahlédněte do našeho článku), už bohužel nedostává odpověď. Je to jistě velká škoda. Nebýt von Neumannovy (ale nakonec i Turingovy) předčasné smrti, mohla se debata o myšlení strojů odvíjet mnoha dalšími zajímavými směry (nehledě na oblasti vědy, do nichž mohl ještě stihnout přispět).
Chceme především upozornit na jeden bod, v němž své kolegy přesáhl. Jeho úvahy nad sebe-reprodukujícím se strojem přesáhly rovinu matematických abstrakcí. Gödelovo číslování i číselný seznam Turingových strojů, který zahrne i číslo univerzálního Turingova stroje, byly skvělé prostředky, jak vyřešit paradox a otevřít distinkci výrazu a obsahu. Von Neumann ale vezme kód a nechá z něj zrodit jeho vlastní kopii, popisnost sebe-reference promění v dynamiku sebe-replikace.
Turing v BBC
Mohlo by se zdát, že Alan Turing z naší rovnice o třech parametrech jaksi vypadl. Britský matematik se jak s Gödelem, tak von Neumannem fyzicky míjel. Nicméně oba zmiňovaní byli s Turingovou prací velice dobře seznámeni. Pro Gödela Turing představoval jistou filozofickou výzvu v otázce pojetí mysli a kognitivních procesů. U von Neumanna se jednalo o profesionální fascinaci univerzálním automatem.
Turing má prvenství zajisté v tom, že vztah myšlení a výpočetního stroje explicitně staví a zaštiťuje pevným myšlenkovým experimentem (který se stal, jak nakonec předvídal, experimentem skutečným). Zároveň, pro nás filosofy, exemplifikuje úlohu analytické filosofie – zaměř se na koncept, promysli jej na dřeň, osekej a vypusť nejen očištěný, ale posilněný soustředěnou perspektivou, zaměřením na klíčový, prozkoumatelný aspekt: model myšlení jako výpočet.
Nakonec nejlépe to vyjadřuje Turing při jedné neakademické a neformální příležitosti, když mluví pro BBC: „Nechci uvádět definici myšlení, ale kdybych musel, asi bych nedokázal říct nic víc než to, že to bylo jakési bzučení, které proběhlo v mé hlavě. Ale opravdu si nemyslím, že bychom se na nějaké definici museli vůbec shodnout. Důležité je pokusit se stanovit hranici mezi vlastnostmi mozku, resp. člověka, o kterých chceme diskutovat, a těmi, o kterých nechceme.“ (Turing, BBC, 1952)
Autoři: Barbora Jurková (Filozofická fakulta Univerzita Palackého), Lukáš H. Zámečník (Filozofická fakulta Univerzita Palackého)
Text vznikl ve spolupráci s časopisem Teorie vědy. Plné znění celého odborného článku si můžete přečíst zde.
- Autor článku: ne










































